Jis laikė šias problemas neprieinamomis to laiko matematikos lygyje. Ir net dabar, po daugiau nei 100 metų, nė viena E. Landau sąrašo problemų nėra išspręsta iki galo.
Garsiausias iš šių keturių uždavinių – Goldbacho problema. Už jos sprendimą vienu metu buvo žadamas ir milijono dolerių prizas.
Teoremos teisingumu neabejojo, bet negalėjo jos įrodyti
„Paprastai suformuluota problema – ne visada paprasta problema. Šis teiginys yra teisingas ir gyvenime ir matematikoje. Likusi daugiau kaip tris su puse šimtmečio neįveikta Didžioji Ferma teorema skambėjo nesudėtingai. Dar paprastesniu atrodo klausimas, kurį Kristianas Goldbachas, beje, buvęs Rusijos mokslų akademijos konferenc-sekretorius ir caro Petro II matematikos mokytojas, uždavė žymiausiam to laiko matematikui Leonardui Euleriui“, – mano I. Belovas.
„Kiekvienas sveikasis skaičius, – rašė jis L. Euleriui, – didesnis už 2, gali būti užrašytas kaip trijų pirminių suma1“. Atsakydamas į šią hipotezę, L. Euleris priminė jų ankstesnį pokalbį, kuriame K. Goldbachas minėjo, kad kiekvienas lyginis skaičius, didesnis už 2, gali būti užrašytas dviejų pirminių skaičių suma.
„Esu įsitikinęs, kad ši teorema yra teisinga, nors negaliu jos įrodyti“, – rašė Euleris.
Hipotezė skilo į dvi dalis
Nuo to laiko problemos statusas beveik nepasikeitė. Šiuolaikinėje matematikoje Goldbacho hipotezė skyla į dvi.
Variantas lyginiams skaičiams, dar vadinamas stipriąja (binarine) Goldbacho hipoteze, skamba taip: „Bet koks lyginis skaičius, didesnis už 2, gali būti išreikštas dviejų pirminių suma“.
Variantas nelyginiams skaičiams, žinomas kaip silpnoji (ternarinė) Goldbacho hipotezė, formuluojamas taip: „Bet koks nelyginis skaičius, didesnis už 5, gali būti išreikštas trijų pirminių suma“.
Apjungia dvi skirtingas charakteristikas
Pasak I. Belovo, Goldbacho hipotezę nedideliems skaičiams nesunku patikrinti. Jis pateikė lentelę, kurioje surašyti visų lyginių skaičių iki 30 Goldbacho skaidiniai ir jų kiekis.
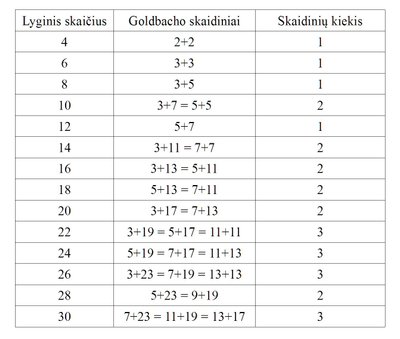
Kaip matome, stiprioji Goldbacho hipotezė lyginiams skaičiams iki 30 yra teisinga. Nilsas Pipingas 1938 m. dar iki kompiuterių eros gerai padirbėjo, patikrindamas hipotezę visiems lyginiams skaičiams iki 100000. 2013 m. Vėliau T. Oliveira de Silva, pasitelkdamas paskirstytus skaičiavimus, patikrino hipotezę visiems lyginiams skaičiams iki 4×1018.
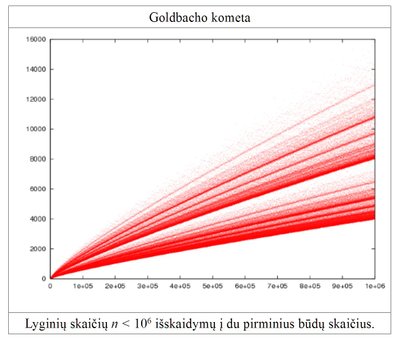
Remiantis negriežtais statistiniais samprotavimais, galima išvesti, kad didėjant skaičiui, turėtų didėti jo Goldbacho skaidinių skaičius. Šį faktą gražiai iliustruoja Goldbacho kometa, kurią gautume horizontalioje ašyje atidėję skaičius, o vertikalioje – atitinkamą jų Goldbacho skaidinių kiekį.
Pagrindinė kliūtis, trukdanti įrodyti Goldbacho problemą, slypi tame, kad ji apjungia dvi labai skirtingas charakteristikas. Pirminiai skaičiai yra apibrėžiami per daugybą, bet hipotezėje kalba eina apie sudėtį. Todėl labai sunku rasti santykį tarp problemos klausimo ir žinomų pirminių skaičių savybių.
Paprastai formuluojama, tačiau iš tikrųjų sunki problema sulaukė net masinės kultūros dėmesio: 2000 m. leidykla „Faber and Faber“, siekdama sudominti Apostoloso Doksiadžio romanu „Dėdė Petrosas ir Goldbacho problema“, pasiūlė milijono dolerio apdovanojimą kiekvienam, kuris per dvejus metus sugebės išspręsti Goldbacho problemą. Nesunku atspėti, kad prizo niekas taip ir negavo: retai kada pavyksta per dvejus metus išspręsti daugiau nei per 250 metus neįveiktą problemą.
Silpnoji Goldbacho hipotezė
Jau yra įrodytos teoremos, leidžiančios tikėtis, kad Goldbacho problema vis dėlto bus išspręsta.
Pirmas proveržis įvyko 1923 m., kai anglų matematikai G. Hardis ir Dž. Litlvudas įrodė silpnąją Goldbacho hipotezę visiems pakankamai dideliems nelyginiams skaičiams. Beje, jų įrodymas rėmėsi kita didžiąja neišspręsta problema – apibendrintąja Rymano hipoteze. Ši hipotezė irgi yra neišspręsta iki šiol, taigi Hardžio ir Litlvudo įrodyme buvo skylė.
1937 m. rusų matematikas I. Vinogradovas gavo įrodymą, nepriklausantį nuo apibendrintosios Rymano hipotezės, ir nustatė, kad visi pakankamai dideli nelyginiai skaičiai gali būti išreikšti trijų pirminių skaičių suma. Formaliai silpnoji Goldbacho hipotezė buvo įrodyta. Už šį pasiekima Vinogradovas buvo apdovanuotas Stalino premija ir gavo Socialistinio darbo didvyrio vardą. Tačiau jo įrodyme trūko atsakymo į klausimą: ką praktiškai reiškia „pakankamai didelis“ nelyginis skaičius?
Po dviejų metų Vinogradovo mokinys K. Borozdinas parodė, kad šiam „pakankamai dideliam“ skaičiui užrašyti prireiktų 6846169 skaitmenų ir kad jis yra per didelis, jei norėtume patikrinti visus už jį mažesnius nelyginius skaičius.
Vėliau ši riba buvo nuolat tikslinama, kol 2013 m. gegužės mėnesį matematikas iš Peru Ch. Chelfgotas, apdovanotas Leverchulmo, Vaitchedo ir Adamso matematinėmis premijomis, patalpino internete (kaip savo laiku Grigorijus Perelmanas, įveikęs vieną iš Tūkstantmečio problemų) 133 puslapių straipsnį, kuriame galų gale buvo įrodyta silpnoji Goldbacho problema. Pagrindinis teiginys skamba taip: visi nelyginiai skaičiai, didesni už 1029, gali būti išreikšti trijų pirminių skaičių suma. Kadangi silpnoji Goldbacho hipotezė jau buvo patikrinta iki 8,875×1030, nes tai anksčiau padarė Chelfgotas ir D. Platas, kartu šie du rezultatai pilnai įrodo silpnąją Goldbacho hipotezę.
Įdomu pažymėti, kad šis darbas rėmėsi kompiuterine matematika dar vienoje vietoje: įrodant Holdbacho hipotezę teko patikrinti jau minėtą apibendrintąją Rymano hipotezę pakankamai dideliam nulių skaičiui. Tai irgi atliko D. Platas.
Stiprioji Goldbacho hipotezė
Stiprioji Goldbacho hipotezė pasirodo – daug sudėtingesnė.
1930 m. rusų matematikui L. Šnirelmanui pavyko įrodyti, kad be galo daug skaičių gali būti išreikšta dviejų pirminių skaičių suma. Be to, jis parodė, kad egzistuoja toks sveikasis skaičius C, kad bet koks natūralusis skaičius yra ne daugiau kaip C pirminių suma. Skaičius C dabar yra žinomas kaip Šnirelmano konstanta.
1995 m. prancūzų matematikas O. Ramare įrodė, kad bet koks lyginis skaičius, didesnis už 4, yra ne daugiau negu šešių pirminių suma.
1973 m. kinų matematikas Č. Czinjunis įrodė, kad bet koks pakankamai didelis lyginis skaičius gali būti išreikštas pirminio ir pusiau pirminio (tai yra arba pirminis, arba dviejų pirminių sandauga) skaičių suma.
Beje, iš jau minėto silpnosios Goldbacho hipotezės įrodymo išplaukia, kad bet koks lyginis skaičius, didesnis už 3, yra ne daugiau kaip keturių pirminių suma. Tačiau kol kas dauguma matematikų mano, kad iki visiško stipriosios Goldbacho hipotezės įrodymo dar toli.





