Vilniaus universiteto Matematikos ir informatikos instituto mokslo darbuotojas Igoris Belovas su DELFI dalijasi viena svarbiausių matematikos problemų, susijusių su pirminiais skaičiais. Taip pat provokuoja: galbūt Jūs sugebėsite atsakyti į klausimus, kuriems atsakymų iškiliausi mokslininkai neranda jau šimtmetį?
1912 m. tarptautiniame matematikų kongrese Kembridže žymus vokiečių matematikas Edmundas Landau paskelbė keturių svarbiausių matematikos problemų, susijusių su pirminiais skaičiais sąrašą. Apie garsiausią iš šių keturių uždavinių – Goldbacho problemą, rašėme čia. Visos keturios E. Landau sąrašo problemos formuluojamos labai paprastai, joms suprasti pakanka elementarių aritmetikos žinių. Tačiau net dabar, po daugiau nei 100 metų, nė viena Landau sąrašo problemų nėra išspręsta iki galo.
„Kompiuterių atsiradimas padarė tikrą perversmą tiek kriptografijoje, tiek kriptoanalizėje – šifrų nulaužimo mene. Kompiuterių gamintojai ir interneto tiekėjai stengiasi sumažinti nepageidautinos prieigos prie vartotojų duomenų riziką, siūlydami vartotojams patikimas šifravimo sistemas. Tarp sukurtų naujųjų šifrų yra gerai žinomas RSA šifras, grindžiamas pirminių skaičių pritaikymu. Aišku, kad ne kiekvienas naujas pirminių skaičių savybių įrodymas gali padaryti įtakos Jūsų banko sąskaitos saugumui, tačiau, be abejo, suteikia galimybių vystyti saugumo temą“, – pasakoja I. Belovas, siūlydamas skaitytojams susipažinti su antrąją sąraše – pirminių dvynių – problema.
Pirminiai skaičiai ir pagrindinė aritmetikos teorema
Didysis XVII a. matematikas ir filosofas Gotfridas Leibnicas sakydavo, jog norint išvesti viską iš nieko, pakanka vieneto. Su šia teze galima sutikti arba nesutikti, tačiau pastebėsime, kad iš vieneto, pasinaudojus sudėties veiksmu, galima išvesti sveikuosius (natūraliuosius) skaičius:
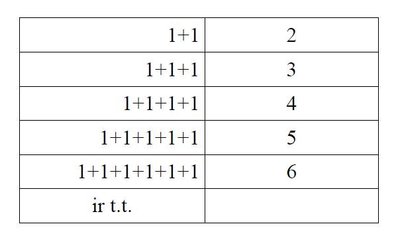
Daugybos atveju plytomis, iš kurių galima „sudaryti“ sveikuosius skaičius, tampa pirminiai skaičiai. Kas gi tie pirminiai skaičiai? Pirminio skaičiaus sąvoka tikrai nesudėtinga: tai sveikas skaičius, kuris dalinasi tik iš savęs ir vieneto. Pirminiai skaičiai sudaro seką: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ... ir taip toliau.
Apie pirminių skaičių svarbą žinojo jau Euklidas. „Pradmenų“ VII-oje knygoje jis rašė: „Jei skaičius yra dviejų kitų sandauga, ir šis skaičius dalinasi iš pirminio, tai ir vienas iš daugiklių dalinasi iš šio pirminio“. Šiame teiginyje jau galima įžiūrėti pagrindinės aritmetikos teoremos ištakas, kurią griežtai suformulavo „matematikų karalius“ Fridrichas Gausas (1801 m): „Kiekvienas natūralusis skaičius, didesnis už vienetą, gali būti išreikštas pirminių skaičių sandauga vieninteliu būdu“:

Pirminiai skaičiai iškyla ten, kur tenka iš vienodų detalių konstruoti taisyklingus objektus. Maiklas Vilersas knygoje „Kasdieninė mūsų algebra“ pateikia įvairių uždavinių, siejančių pagrindinę aritmetikos teoremą su kasdienybės problemomis. Štai vienas iš jų loginių galvosūkių mėgėjams:.
Miesto taryba tik ką pradėjo miesto aikštės rekonstrukciją. Aikštės matmenys yra 602×322 pėdų, o miesto taryba nori išgrįsti visą plotą kvadratinėmis plytelėmis. Tarybos nariai nori, kad šios plytelės būtų kiek galima didesnės – nė negalvokite siūlyti 193844 vienos kvadratinės pėdos pločio plytelių. Ar galite surasti didžiausios įmanomos kvadratinės plytelės matmenis, kad tokias plyteles būtų galima panaudoti visai aikštei iškloti, nė vienos nesupjaustant?
Atsakymas – straipsnio pabaigoje.
Pirminiai skaičiai ir pirminiai giminaičiai
Jei įdėmiai pažvelgtume į pirminių skaičių seką, pastebėtume, kad tarp jų pasitaiko tokių, kurie yra labai artimi ir skiriasi tik dvejetu: 3 ir 5, 5 ir 7, 11 ir 13, 17 ir 19, 29 ir 31, 41 ir 43, 59 ir 61, 71 ir 73, ir t.t. Tokios poros yra vadinamos pirminiais dvyniais, o jų skaičius yra viena iš didžiausių matematikos mįslių.
Tad pirminių dvynių problema skamba taip:
Ar pirminių dvynių yra be galo daug?
Beje, galima nagrinėti kitokius pirminius giminaičius, pavyzdžiui, pirminius trynukus. Pirminių skaičių trynuku vadinamas pirminių skaičių trejetas, kuriame antrąsis didesnis už pirmajį dviem vienetais ir mažesnis už trečiąjį taip pat dviem.
Taigi, pabandykite atsakyti:
Ar pirminių trynukų yra be galo daug?
Atsakymą galite rasti taip pat straipsnio pabaigoje.
Panagrinėkime pirminius dvynius. Imkime ir užrašykime dvynių porų „centrus“.
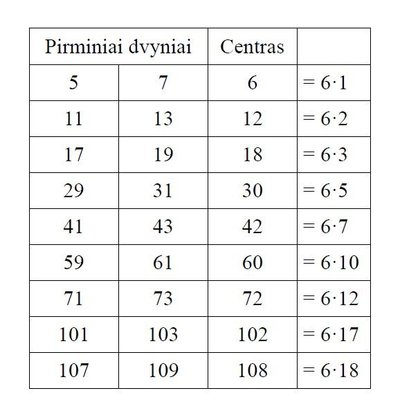
Nuostabus dalykas: visi dvynių „centrai“ lentelėje yra šešeto kartotiniai, ir ši savybė galioja ne tik pirmam dvynių dešimtukui. Galima pastebėti, jog visi pirminiai dvyniai lentelėje yra pavidalo (6n-1, 6n+1), čia n yra kažkoks natūralusis skaičius ir dar turi baigtis 0, 2, 3, 5, 7, arba 8...
Siūlome skaitytojams įrodyti patiems, pasinaudojus dalybos iš 6 liekanų savybėmis, kad ši išvada yra teisinga visoms dvynių poroms. Atsakymą taip pat rasite straipsnio pabaigoje.
Ženkime toliau:
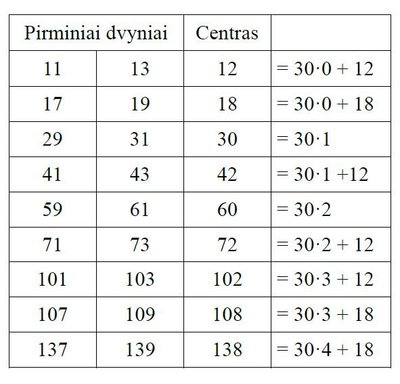
Taigi, jei dar atsižvelgtume į dalumą iš 5 (5·6 = 30) , tai pasirodo, kad visos dvynių poros (be pirmų dviejų) dalijasi iš 30 su liekanomis (11, 13), (17, 19) arba (29, 31). Be to, buvo įrodyta, kad natūraliųjų skaičių pora (n, n + 2) yra pirminių dvynių pora tada ir tik tada, kai 4(n-1)!+4 = n(n+2)m – n , čia m yra tam tikras sveikasis skaičius, o (n-1)! žymi, kaip įprasta matematikoje, skaičių nuo 1 iki n-1 sandaugą.
Pirminiai skaičiai ir begalybė
Jau Euklidas žinojo, kad pirminių skaičių yra tiek pat, kiek natūraliųjų, t.y., be galo daug. Apie skaičių sekų savybes galima daug pasakyti, nagrinėjant atvirkštinių tiems skaičiams sumas. Žymus XVIII a. matematikas Leonardas Euleris pažvelgė į pirminių skaičių begalybės problemą iš šios pusės. Jis nagrinėjo skaičių, atvirkštinių pirminiams, sumą:

Aišku, jei pirminių skaičių skaičius yra baigtinis, tai ir atvirkštinių jiems suma bus baigtinė. Pastaruoju atveju ši suma darg būtų racionalioji trupmena, t.y., išreiškiama dviejų sveikųjų skaičių santykiu. Euleris įrodė, kad aukščiau užrašyta suma yra begalinė. Taigi, jo įrodymas patvirtino, kad pirminių skaičių yra be galo daug. Jei šį faktą palygintume su kitu Eulerio rezultatu: skaičių, atvirkštinių sveikųjų skaičių kvadratams, suma yra baigtinė (Euleris įrodė, kad ši suma yra lygi π2/6. Ir čia – aritmetikoje – skaičius pi! Nuostabus rezultatas) seka, kad pirminiai skaičiai pasitaiko dažniau, nei kvadratai!
Pirmas proveržis įvyko, kai norvegų matematikui Viggo Brun įrodė 1919 m., jog skaičių, atvirkštinių pirminiams dvyniams, suma yra baigtinis skaičius.
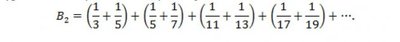
Ši suma, vadinama Bruno konstanta, artėja prie 1.90216... Įdomu, kad nors mes nežinome, ar šioje sumoje yra baigtinis ar begalinis dėmenų skaičius, vis tiek galime apskaičiuoti jos reikšmę tokiu tikslumu, kurį leidžia turimi kompiuterių resursai. Tačiau taip pat nežinoma, ar šis skaičius yra racionalusis ar iracionalusis. 1994 metais, skaičiuodamas kompiuteriu Bruno konstantą amerikiečių matematikas Tomas Naislis atrado gedimą Intel Pentium luste. Korporacija apie tai žinojo, bet apie galimą gedimą nepranešė. Atradimas sukėlė didelį skandalą, kuris kainavo Intel korporacijai 475.000.000 dolerių dėl gražinamų lustų. Beje, Bruno konstantos skaitmenys – $1.902.160.540 – buvo panaudoti Google pasiūlyme Nortelo patentų aukcione 2011 metais (tiesa, laimėti tai nepadėjo).
Didžiausių pirminių dvynių paieškos ir skaitiniai eksperimentai
Iš Bruno rezultato aišku, kad net jei pirminių dvynių yra be galo daug, jie pasitaiko gana retai. Tačiau kiek retai? Britų matematikai Hardis ir Litlvudas iškėlė hipotezę, jog dvynių pasirodymo dažnis intervale, neviršijančiam pasirinktą skaičių, yra atvirkščiai proporcingas šio skaičiaus logaritmo kvadratui. Tačiau ši hipotezė taip pat dar nėra įrodyta.
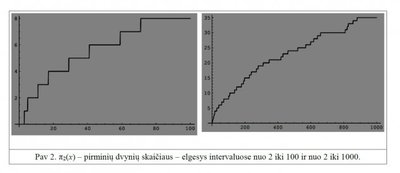
Pav. 2 pavaizduotas pirminių skaičių skaičius įvairiuose intervaluose. Matyti, kad didėjant intervalui galima pastebėti atsirandant intervalų, kuriuose dvynių skaičius nekinta. Jei didžiausia dvynių pora egzistuoja, šis grafikas prie didelių skaičių turi nustoti kisti.
Netikėtą atradimą pirminių skaičių pasiskirstyme padarė visai mokslo srityse iki tol nežinotas vyriškis. Kinų kilmės p. Yitang Zhangas (g. 1955) ilgai nerado darbo ir dirbo amerikiečių sumuštinių „Subway“ užkandinėje. Netgi įgijęs 1985 m. Pekino universitete magistro laipsnį matematikos srityje, o 1991 m. apgynęs Purdue universitete (Italija) daktaro laipsnį, jis ir toliau ilgokai dirbo „Subway“ tinkle.
O toliau viskas nutiko taip – jis pradėjo nagrinėti laikytą neišsprendžiama pirminių dvynių begalinio kiekio problemą, ir savo sprendimą 2013 m. pasiuntė žurnalo „Annals of Mathematics“ redakcijai. Ten iškart suprato, kad gavo genialų darbą, įrodantį svarbią pirminių skaičių pasiskirstymo teoremą. Po savo straipsnio paskelbimo Yitang Zhangas buvo apdovanotas daugeliu matematinių premijų: 2013 m. - Morningside ypatingų pasiekimų premija ir Ostrowski‘o premija; 2014 m. Frank Nelson Cole premija skaičių teorijos srityje, Rolf Schock‘o premija ir MacArthur‘o premija, 2014 m. jis buvo išrinktas Taivanio „Academia Sinica“ nariu, ir tais pačiais metais buvo paskirtas New Hampshire universiteto profesoriumi. Jis pateikė įrodymą, kad yra be galo daug pirminių skaičių porų, besiskiriančių tam tikru skirtumu. Dabar ši ribinis skirtumas yra sumažintas iki 246. Belieka sumažinti jį iki 2.
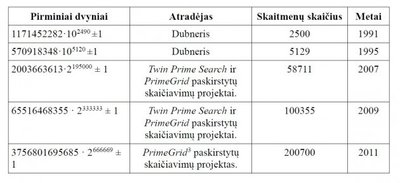
Kol teoretikai aiškinasi, ar pirminių dvynių skaičius yra baigtinis skaičius, ar jų be galo daug, eksperimentatoriai ieško didžiausios dvynių poros. Stiprų impulsą kompiuterių eksperimentams su pirminiais skaičiais davė savanoriškas paskirstytų skaičiavimų projektas „PrimeGrid“ (projekto įkūrėjas yra Rytis Slatkevičius), pradėtas 2005 m. Projektas naudoja Berklio universiteto platformą „BOINC“, leidžiančią visiems pageidaujantiems prisijungti prie projekto su savo kompiuteriu. Šiuo metu projekte dirba daugiau nei 6100 dalyvių iš 189 šalių, kurie pajungė pirminių skaičių tyrimams daugiau nei 10000 kompiuterių. Kompiuterinių technologijų progresas duodą didžiulį impulsą skaičiavimas, ir rezultatai, kaip matyti iš lentelės, sparčiai auga.
Yra paskaičiuota, kad intervale nuo 2 iki 1018 yra 808.675.888.577.436 dvynių porų. Taigi šiuolaikiniams pirminių skaičių konkistadoriams vieno (net galingo) kompiuterio yra per mažai – tenka apdoroti gigantiškus kolosalių skaičių kiekius, pasitelkiant lygiagrečius ir paskirstytus skaičiavimus.
Ar pastangos yra vertos sugaišto kompiuterių ir tyrėjų laiko? Tikrai taip, nes kol nėra įrodyta priešingai, kiekviena nauja pirminių dvynių pora gali būti paskutinė.
Uždavinių atsakymai
Miesto aikštės rekonstrukcija. Turime, kad 602 = (2×7)×43, 322 = (2×7)×23. Taigi, 2×7 = 14 yra didžiausias kvadratinių plytelių, kuriomis galima išgrįsti aikštę, kraštinės ilgis.
Nustatant pirminių trynukų skaičių, pastebėsime, jog tarp trijų, vienas po kito einančių ir besiskiriančių dvejetu, skaičių (p, p+2, p+4) vienas turi būtinai dalintis iš 3. Kadangi visi trys skaičiai turi būti pirminiai, atsiras tik vienas pirminis trynukas (3, 5, 7).
Įrodysime, jog pirminių dvynių „centrai“ (išskyrus pirmąjį – tarp 3 ir 5) yra šešeto kartotiniai. Iš tikrųjų, jei pirminiai dvyniai (tai visada nelyginiai skaičiai) yra 2n-1 ir 2n+1 , tai jų centras yra 2n – lyginis skaičius. Vienas iš trijų iš eilės einančių sveikųjų skaičių – 2n-1, 2n, 2n+1 – visada yra trejeto kartotinis, ir tai yra 2n, nes kiti du yra pirminiai, didesni už 3. Taigi centras dalinasi ir iš 2, ir iš 3, reiškia, ir iš 6.




